Решение заданий по математике




Решение заданий по математике, подготовка к ЕГЭ


Задание 1

Решите уравнение:

1/cos2x + 3tgx - 5 = 0. Укажите корни, принадлежащие отрезку [-π;  π/2].

Решение:

1) Запишем уравнение иначе:
(tg2x+1)+ 3tgx - 5 = 0;
tg2x + 3tgx - 4 = 0;
tgx = 1 или tgx = -4.
Следовательно, x=π/4 + πk или x = -arctg4 + πk. Отрезку [-π;  π/2] принадлежат корни -3π/4, -arctg4, π/4.
Ответ: -3π/4, -arctg4, π/4.


Задание 2

Дана правильная треугольная призма ABCA1B1C1, сторона основания которой равна 2, диагональ боковой грани . Найти угол между плоскостью A1BC и плоскостью основания призмы.

Решение:

Обозначим середину ребра BC буквой H. Отрезки AH и A1H перпендикулярны BC, так как треугольник ABC - равносторонний, а A1BC - равнобедренный. Следовательно, угол A1HA - линейный угол двугранного угла с гранями BCA и BCA1.

Рассмотрим треугольник A1AB: по теореме Пифагора найдем AA1=1.

Рассмотрим треугольник AHB: по теореме Пифагора найдем AH=.

Из треугольника HAA1 находим:

 

Отсюда находим: угол A1HA=30o.

Ответ. 30о.


Задание 3

Решите неравенство:

Решение:

Преобразуем неравенство:

  

Найдем, при каких значениях х левая часть имеет смысл:

 

 

Получаем:  или   

Значит, при всех допустимых значениях x. Поэтому,

 

Сделаем замену . Получаем:

 

Таким образом,

 

откуда 

 

Решив полученное квадратное уравнение, найдем корни: -6 и -1. Условию   или    удовлетворяет только x=-1.

Ответ. -1.


Задание 4

Дан угол ABC, равный 30о. На его стороне BA взята точка D такая, что AD=2 и BD=1. Найти радиус окружности, касающейся прямой BC и проходящей через точки A, D

Решение:

Центр О искомой окружности принадлежит серединному перпендикуляру к отрезку AD. Обозначим буквой p середину AD, буквой Q - основание перпендикуляра, опущенного на прямую BC из точки O, буквой E - точку пересечения прямой BC и серединного перпендикуляра. Отрезки OA, OD, OQ равны радиусу R окружности.

Заметим, что точка O не может лежать по ту же сторону от прямой AB, что и точка E, так как в этом случае расстояние от точки O до прямой BC меньше, чем расстояние от нее до точки A.

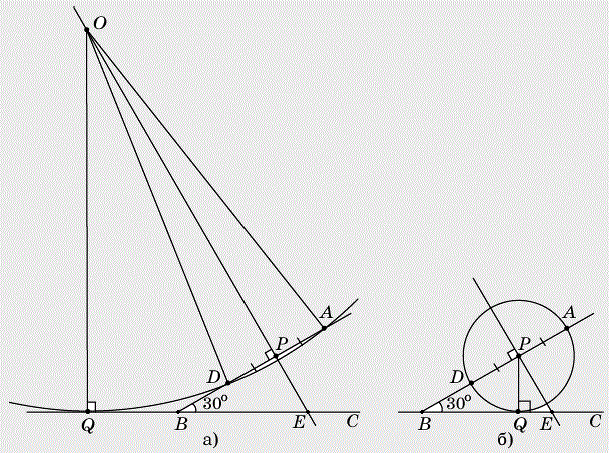
ЕГЭ по математике

Из прямоугольного треугольника BpE с катетом Bp=2 и углом B=30o находим, что 

  

Так как OA=R и Ap=1, получим:

и, следовательно, 

 

Из прямоугольного треугольника OQE, в котором угол E=60o, находим:

 

Таким образом, получаем следующее уравнение для R:

 

Данное уравнение легко приводится к квадратному возведением в квадрат левой и правой частей и приведением подобных членов.

 

Решив данное уравнение, получим R1=1, R2=7.

Ответ. 1 или 7.


Задание 5

Найти все значения параметра при которых уравнение

 

имеет хотя бы один корень.

Решение:

Запишем уравнение в следующем виде: 

.

Функция непрерывна и

1) неограниченно возрастает , так как при любом раскрытии модулей будем иметь:

 

где  

2) убывает, так как при любом раскрытии модулей будем иметь:

 

где  .

Следовательно, свое наименьшее значения функция  примет, а уравнение имеет корень тогда и только тогда, когда

Решим это неравенство:

 

Ответ. .


Задание 6

Найдутся ли хотя бы три десятизначных числа, делящихся на 11, в записи каждого из которых использованы все цифры от 0 до 9?

Решение:

Число делится на 11 тогда и только тогда, когда разность между суммами его цифр, стоящих на нечётных и на чётных местах, делится на 11. Запишем все цифры подряд:9876543210. В написанном числе указанная разность сумм равна 5.
Меняя местами, например, 5 и 8, мы одну сумму увеличиваем на 3, а другую уменьшаем на 3. Значит, разность между суммами его цифр, стоящих на четных и на нечетных местах, становится равной 11. Меняя местами, например, 4 и 7, или 3 и 6, получаем требуемые примеры.
Примечание: В задаче требуется нахождение всех чисел, обладающих указанным свойством.