ЕГЭ по математике №16 C4

ЕГЭ по математике №16 C4

ЕГЭ по математике №16 C4 с решением и ответами

ЕГЭ по математике №16 C4 с решением и ответами

ЕГЭ по математике №16 C4 решение.

ЕГЭ по математике №16 C4.

Хорда окружности, описанной вокруг треугольника

Условие:

Радиус окружности, описанной около ∆ АВС, равен 13, Cos ВАС = - 5/13. Высота, проведённая к стороне ВС, равна 5. Найдите длину той хорды АМ описанной окружности, которая делится пополам стороной ВС.

Решение:

1. Во-первых, найдем BC. Как известно, угол, вписанный в окружность, опирается на вдвое большую дугу. Обозначим угол BAC за "альфа" (его косинус мы знаем). Тогда дуга BC (большая) равна 2альфа, а угол BOC, соответственно, 2пи-2альфа.

Хорда BC = 2R*sin(BOC/2) = 2*R*sin(пи-альфа) = 2*R*sin(альфа) = 2*R*sqrt(1-(5/13)^2) = 2*13*12/13 = 24.

2. Из прямоугольного треугольника BKO находим KO = sqrt(13^2-12^2) = 5

3. Теперь нам пора заметить, что у нас опять два случая. Как обычно, обозначим их красным и синим. Рассмотрим красный, а синий получится сам собой.

4. Из точки D отложим отрезок DP, параллельный и равный AT=5. KO=DP, оба они перпендикулярны BC...
В общем, я веду к тому, что точки M, O и P лежат на диаметре, параллельном BC, а треугольники ADT и DMP равны.

5. Рассмотрим прямоугольные треугольники ODM и Atd. Углы ADT и OMD равны, а значит, эти треугольники подобны (по двум углам).
Можем составить пропорцию:

OM/DM = AD/td. Кстати, обозначим DM за x (То есть, в окончательном ответе нам нужно будет указать 2x).
Итак, 13/x = x/td.

В свою очередь, td найдем из треугольника Atd:
td = sqrt(x^2-25)

Итак, вот и получилось уравнение:
13/x = x/sqrt(x^2-25)
Оно сводится к биквадратному
x^4-169*x^2+4225 = 0

У него есть два положительных корня:
x1 = sqrt(13/2*(13+sqrt(69))) (это для "красного" случая)
x2 = sqrt(13/2*(13-sqrt(69))) (это для "синего" случая)

Надо ещё умножить на два.

Ответ:

2*sqrt(13/2*(13+sqrt(69))), 2*sqrt(13/2*(13-sqrt(69)))

ЕГЭ по математике №16 C4.

Условие:

Трапеция ABCD
Площадь её = 90
AD=2BC
P - середина AD
Диагонали пересекаются в точке О и также пересекают отрезки PB и PC в точках М и N.
Найти площадь OMNP

Решение:

ABCP и PBCD - параллелограммы с одинаковыми основаниями и высотами, точки M и N - точки пересечения их диагоналей.
Это значит, что MN параллельно BC. Это вроде бы очевидно, но тем не менее.
И из этих же соображений мы в два счета доказываем, что MN = BC/2

Четырехугольник OMNP состоит из треугольников OMN и PMN с общим основанием MN. Значит, его площадь равна сумме их площадей и равна MN, помноженной на сумму высот этих треугольников пополам.
А сумма их высот - это расстояние от точки O до AD.

Вот и найдем это расстояние. Мы знаем, что треугольники AOD и COB подобны (по трем углам), а BC и AD относятся как 1:2. Значит, и высоты этих треугольников относятся как 1:2, и получается, что расстояние от O до AD равно 2/3 высоты трапеции.

То есть, если известная нам площадь трапеции равна
S = h*(AD+BC)/2 = 3/2*h*BC,
то искомая площадь четырехугольника равна

(2/3*h)*(BC/2)/2 = h*BC/6 = S/9 = 10

Ответ: 10

ЕГЭ по математике №16 C4

Дан угол ABC, равный 30^о. На его стороне BA взята точка Dтакая, что AD=2 и BD=1. Найти радиус окружности, касающейся прямой BC и проходящей через точки A, D

Решение:

Центр О искомой окружности принадлежит серединному перпендикуляру к отрезку AD. Обозначим буквой P середину AD, буквой Q - основание перпендикуляра, опущенного на прямую BC из точки O, буквой E - точку пересечения прямой BC и серединного перпендикуляра. Отрезки OA, OD, OQ равны радиусу R окружности.

Заметим, что точка O не может лежать по ту же сторону от прямой AB, что и точка E, так как в этом случае расстояние от точки O до прямой BC меньше, чем расстояние от нее до точки A.

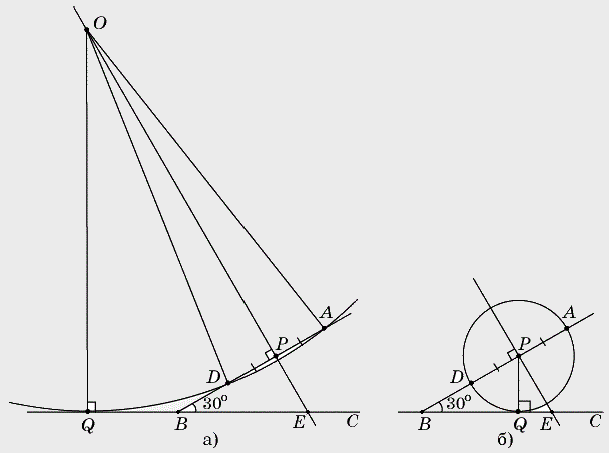
ЕГЭ по математике